(Capítulo 5, Problema 17 - Halliday \ Resnick e Wlaker - 10ª ed., v 1)
Uma questão clássica de mecânica, e como sempre vamos ler primeiro e retirar os dados explícitos do problema, geralmente são os matemáticos. Bem como o que o problema deseja de nós.
Dados explícitos:
massa (m) do bloco = 8,5 kg
ângulo θ = 30°
Consideraremos g = 9,81 m/s^2
(a) a tração da corda
(b) a força normal que age sobre o bloco
(c) Determine o módulo da aceleração do bloco se a corda for cortada.
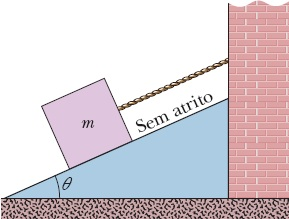
Com os dados separados, faremos novamente um segunda leitura, desta vez procurando as informações implícitas na questão. Colocações da Física, envolvida, para nos guiar ao uso correto dos dados matemáticos. E de cara, identificamos o plano inclinado que nos leva a decomposição de forças e a um sistema que as envolvem. Conforme a figura abaixo, que será nossa guia na resolução do problema.
Partimos então para o item (a) que pede a tração na corda, que observamos pela decomposição de forças que encontra-se no eixo x. e que sabemos que como o sistema esta em equilíbrio, a somatória é igual a zero. Logo temos que,
Px - Tcorda = 0 :. P . cosθ - Tcorda = 0 :.
m . g . cos 60º - Tcorda = 0
Tcorda = 41,69 N
O item (b) que saber o valor da normal (N), e vocês lembram onde ela esta e a condição para sua existência. Lembrando que o sistema esta em equilíbrio. Então temos que,
N - Py = 0 :. N = Py :. N = P . sen θ :. N = m. g . sen 60º
N = 72,21 N
Agora ele considera "cortar a corda" e pede a aceleração do corpinho descendo a rampa. E sabemos que não esta sendo considerado o atrito, que fique claro isso. Logo temos que,
F - Px = 0 :. F = Px :. m . a = m . g . cos 60º
a = 4,91 m/s^2
Perceberam o quanto simples é a questão quando seguimos uma sequência didática clara.
Até a próxima!
Esperamos ter ajudado em algo.




0 Comentários
Deixe aqui sua SUGESTÃO, DÚVIDA! Isso ajuda a criar e melhorar (novos) conteúdos.